Queue (큐)
- 개념 : 각 요소에 우선순위를 부여하는 데이터 구조의 한 종류이다.
- 인큐(enqueue): 큐에 요소를 추가하여 큐 뒤쪽에 배치하는 것
- 데큐(dequeue) : 큐에 가장 오랫동안 있던 요소를 삭제하는 것
- 큐는 선입 선출(First In First Out, FIFO) 데이터 구조 이다.
- 가장 먼저 추가된 요소가 우선적으로 삭제됨
- 스택(stack)은 후입선출
Priority Queue (우선순위 큐)
- 키와 값의 체계를 사용해 큐의 요소들을 정렬한다.
- 우선순위 큐에서 모든 요소는 우선순위가 있으며 이는 키에 해당한다.
- 우선순위가 높은 요소는 우선순위가 낮은 요소보다 먼저 삭제된다. (같다면 먼저 들어온것 부터)
- 메소드 : 요소 추가하기, 요소 삭제하기, 우선순위가 높은 요소 가져오기, 큐가 가득 찼는지 확인하기
- 구현 방법 : 배열, 연결 리스트, 힙(추천)
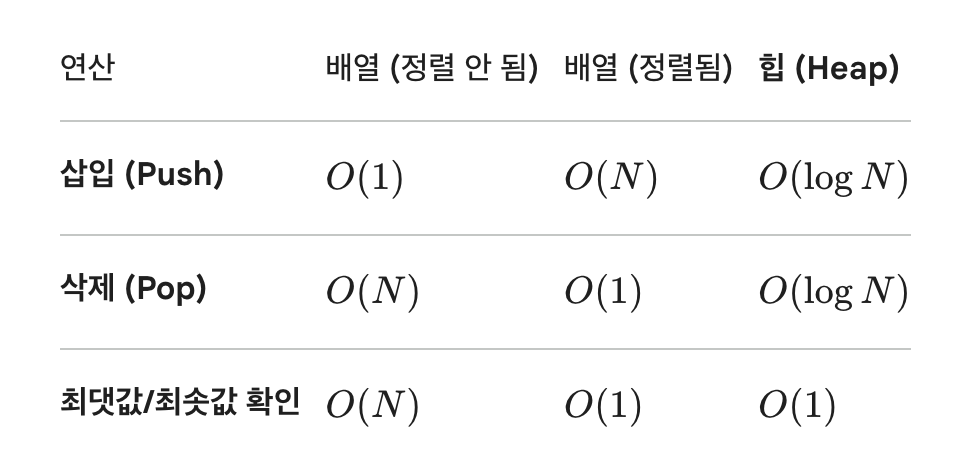
Heap(힙)
- Heap : 완전이진트리 형태의 자료구조
- 최대 힙(Max Heap) : 부모 노드의 키 값이 자식 노드보다 큰 구조
- 최소 힙(Min Heap) ; "기본 형태" : 부모 노드의 키 값이 자식 노드보다 작은 구조
- 배열로 힙을 표현할 때
- 왼쪽 자식 노드의 인덱스 = 부모 노드의 인덱스 x 2
- 오른쪽 자식 노드의 인덱스 = 부모 노드의 인덱스 x2 + 1
- 부모 노드의 인덱스 = 자식 노드의 인덱스 // 2
- IF. python에서 0을 시작(Root node)으로 하면 떄문에 왼쪽과 오른 쪽 노드가 반대.

우선순위 큐의 동작 원리
- 삽입 연산
- 트리의 말단 노드에 새로운 값을 삽입한다.
- 말단부터 루트까지 트리를 거슬러 올라가면서 Heapify(up-heap) 작업을 수행한다.
- Heapify : Heap의 특성을 만족하도록 각 노드들의 위치를 조정하는 과정
- 삭제 연산
- 루트 노드를 삭제한다.
- 말단 노드를 빈 자리에 가져온다.
- 루트를 말단까지 내려가면서 Heapify (down-heap) 작업을 수행한다.
Python 구현 모듈 추천
- Queue 구현 : from collections import deque
- Heap 구현 : import heapq
- 최소 우선순위 큐(Min-Priority Queue)가 기본 형태
- 최대 우선순위 큐(Max-Priority Queue)를 위해서는 값에 마이너스(-) 추가
import heapq
# 1. 힙 생성 및 요소 추가 (heappush)
pq = []
heapq.heappush(pq, 10)
heapq.heappush(pq, 5)
heapq.heappush(pq, 20)
heapq.heappush(pq, 1)
# 2. 우선순위가 높은(가장 작은) 요소 확인
print(pq[0]) # 출력: 1
# 3. 요소 삭제 및 반환 (heappop)
print(heapq.heappop(pq)) # 출력: 1 (가장 작은 값)
print(heapq.heappop(pq)) # 출력: 5
# 4. 기존 리스트를 힙으로 변환 (heapify)
numbers = [4, 1, 7, 3, 8, 5]
heapq.heapify(numbers)
print(numbers) # 힙 구조로 재배치됨- heappush(heap-object) : 데이터 삽입(up-heap) ; O(logN) => 트리의 위쪽으로 올라가면서 비교
- 1. 트리의 가장 마지막 노드(배열의 맨 끝)에 새로운 item 추가
- 2. 부모와 비교&교환 과정을 반복하여 힙의 구조를 유지
- heappop(heap-object) : 데이터 삭제(down-heap) ; O(logN) => 트리의 아래로 내려가면서 비교
- 1. 트리의 루트 노드를 꺼내고
- 2. 트리의 가장 마지막 노드(배열의 맨끝)를 루트 자리(Index=0)로 옮기고
- 3. 자식과 비교하여 작다면 바꾸는 작업 반복하여 힙의 구조를 유지
우선순위 큐의 활용
- 운영체제의 작업 스케줄링
- Heap Sort (힙 정렬)
- 허프만 코딩
- 다익스트라 알고리즘 (그래프 최단 거리)
관련 개념 문제 추천
----------------참고자료---------------
* [도서] 코드 없는 알고리즘과 데이터 구조
* [블로그] 우선순위 큐, 이창윤 (링크)
--------------------------------------
'프로그래밍 > Coding' 카테고리의 다른 글
| [기초문법] zip()의 활용 (feat. 행렬 전치) (0) | 2026.01.19 |
|---|---|
| [기초문법] Python Counter object (0) | 2026.01.16 |
| [기초문법] sys.stdin ; 3 method ; in python (1) | 2026.01.12 |
| [기초문법] sys.stdin.readline (feat. input()) (0) | 2025.12.29 |
| [자료구조] 깊이우선탐색(DFS) vs 너비우선탐색(BFS) (0) | 2025.02.02 |



